货代航线的直线分布

      假设f(VOTn）服从直线分布，它的一般表达式为f(VOTA）=A×VOTA+B,将这个表达式代人式当中可得
VOTi(j+1)AO
f=J
(AxVOTA +B)d VOTA
JvoTjAo
=A(VOTRGH)n0 -VOTno)+B(VOTiGH)Xo -VOT,Ao)(2-50)
oijH)O vOT,A(A x VOTA +B)d VOT,A

此时VOTn=VoTzno

       式中：A，B—不同VOT的旅客数量与VOT的关系参数。但我们如何确定A、B呢?事实上根据式只能知道A和B的关系，而不能得到A、B的数值，所以代人式中不能得到需要的结果。于是，我们从直线的几种特殊情况出发，通过有关假设可得到有关结论。

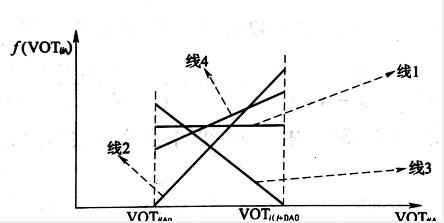
       (1)讨论一：假设A=0，即得到普通均匀分布的情况，其分布图像如中的线1。当A=0时，根据式可以知道

B=

VOTiC4)m-VOT%这样就知道了A和B的具体值，将它们代人式
f
        后可以算出
VOT,m=YOTc)no + VOTno
        根据式算出了第i条货代公司航线第j种票价下旅客的时间价值，知道这个值之后，再运用加权平均值法，即
VOTA=E,VOTA
       式中：f—第j种票价下旅客所占比例。根据式可以得到每条货代公司航线下旅客的时间价值。要得到民航旅客的时间价值，就要再用加权平均的方法，即
EV.xVOTA
VOT =
Ev.
       式中：N—第i条货代公司航线上的年旅客运输量。
      (2）讨论二：假设当VOTA=VOTAo时，f(VOTA0）=0，其分布图像如中的线2，即
B=-AxVOTAm
      根据式和式可以解出A和B的值，分别为
2f
-2f×VOTiAo
A=(VOT.)m-VOT,%1B
(VOTGH)Ao -VOTinm)
      然后代人到式中，即可以求出这类旅客的时间价值表达式
VoTA=2VOTRa)g-NOTwo X VBiw.ne -VOTRe
3(VOTo:1)Ao -VOTAo)
       根据式即可得到每条货代公司航线每种折扣上民航旅客的时间价值。最后根据式和式依次得出每条货代公司航线上旅客的时间价值和民航旅客的时间价值。
     （3)讨论三：假设当VOTA=VOTj-1)0时，f(VOT心l)%）=0，其
       分布图像如中的线3，即
B=-AxVOTiol)no
       同样运用讨论二中的方法可以求出民航旅客的时间价值的表达式为
vOTmsYOTRu)o +VOTAo X VOTua)o -2VOTu
3(VOTo+l)Ao -VOTAo)
       根据式即可得到每条货代公司航线每种折扣上民航旅客的时间价值。最后根据式和式依次得出每条货代公司航线上旅客的时间价值和民航旅客的时间价值。
      （4）讨论四：假设f(VOTA）跟f的比例相符，分布图像如中的线4，即
A x VOTii)no +B fo)
AxVOTAO+B~f
        那么根据式(2-50）和式(2-59）可以算出A和B的值，分别为
2f(fo) -f)
A=
T(VOTGH)Ao -VOTEAo)(fo1)-f)+
12(VOTcH)no ×f-VOTino ×fiu))(VOTit)Ao -VOTiA0)
Bs1×(VOTici)no Xf-VOTino xfi))
fou)-f
       然后将A和B的值代入式中，推导出VOTA的表达式为
TVOTi.)o6(2fGa)+)-VOT,m XVOTGwofG) -)1
VOTEo(fiu)+2,)
Vom=3I(VoT.e +VOT,m)G.) -5j)+2(VOTw.ayo,-VOT,o /Gm)1
       最后根据式和式依次得出每条货代公司航线上旅客的时间价值和民航旅客的时间价值。以上从4个特殊的方面讨论了直线分布的情况，讨论一主要从均匀分布考虑，讨论二和讨论三主要从两个极限斜率值来考虑，讨论四则从原函数的比例出发，它们各自代表一种特殊情况。从假设当中可以得到，讨论一和讨论四的结果应该处于讨论二和讨论三两个结果的中间。