(1)最大化:max[f(c)-ac] 港口最优装运量发生在港口的边际产量MP等于它的标准综合单位成本a 时,MP(c')=a
(2)前提分析 第一,如果港口的边际产量大于a,那么在港口增加货物运输数量是有利的 如果港口的边际产量小于a,那么减少装运数量是有利的。 第二,我们把港口作为公共设施管理时,需要达到效率。当该城市再增一标准 综合单位商品时,总产量会增加至: f(c+1) 那么该单位标准综合货物可能为城市带来的平均收益将是: f(c+1)/(c+1) 这样,逻辑上说,该城市每个经营者应该算一笔账,就必然将每标准综合单位 的货物的平均收益与平均生产或购买成本相比较。
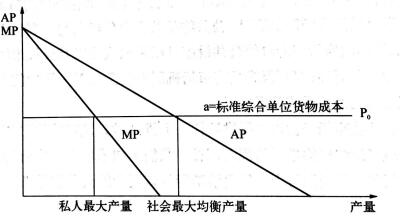
(3)如果f(c+1)/(c+1)>a,增加每标准综合单位货物的运量是有利可 图的。
(4)因此,在每标准综合单位货物的平均利润等于零以前,该城市应该会对港 口装运货物运输作出继续使用的选择,并继续增加货物运量。
(5)但是,一个城市的所有跨境物流从业者往往是盲目的,而这种理性是做不到的! 值得思考的是,政府对港口这种公共设施的管理,以何种方式达成效率就成了必要。
简要模型分析与说明
(1)分析过程当个人进行成本收益分析时,他所关注的是超额价值,并把价 值同成本作出比较。对他来说,这样考虑是够精细的,然而却忽略了一个事实,即 随着港口货物运量的增加,将使港口形成堆积与拥挤,整体效率下降,可变成本提 高,这会使所有商品成本提高,从而所有商品的收益都会下降。 因为,上一阶段的分析上,虽然作出的逻辑性、理性分析看似合理,但是忽略了 港口运输行为的社会成本,即在港口堆放与运输货物数量太多,不仅增加每标准综 合单位货物的成本,也会使港口效率与货物收益下降,无度的公共使用与放任自 流,缺乏管理,甚至可能使港口因为拥挤堆积,效率降低乃至废弃。同时,该港口城 市发展也受到影响。
(2)边际分析模式我们就该问题作出边际分析模型,以决定 最大均衡产量的位置。 随着货物的增加,每标准综合单位货物的平均产量曲线呈递减趋势。由于平 均产量曲线呈递减趋势,边际产量曲线始终位于平均产量曲线下方。


